LOGARITMOS EN LA SISMOLOGÍA:
La escala sismológica de Richter, también conocida como escala de magnitud local(ML), es una escala logarítmica arbitraria que asigna un número para cuantificar la energía liberada en un terremoto.
La sismología mundial usa esta escala para determinar la magnitud
de sismos de entre 2,0 y 6,9 grados y de 0 a 400 kilómetros de
profundidad.
Richter reportó inicialmente valores con una precisión de un cuarto de unidad, sin embargo, usó números decimales más tarde.
donde:
 = amplitud de las ondas en milímetros, tomada directamente en el sismograma.
= amplitud de las ondas en milímetros, tomada directamente en el sismograma.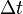 = tiempo en segundos desde el inicio de las ondas P (Primarias) al de las ondas S (Secundarias).
= tiempo en segundos desde el inicio de las ondas P (Primarias) al de las ondas S (Secundarias).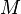 = magnitud arbitraria pero constante a terremotos que liberan la misma cantidad de energía.
= magnitud arbitraria pero constante a terremotos que liberan la misma cantidad de energía.
El uso del logaritmo en la escala es para reflejar la energía que se desprende en un terremoto. El logaritmo incorporado a la escala hace que los valores asignados a cada nivel aumenten de forma logarítmica, y no de forma lineal. Richter arbitrariamente escogió un temblor de magnitud 0 para describir un terremoto que produciría un desplazamiento horizontal máximo de 1 μm en un sismograma trazado por un sismómetro de torsión Wood-Anderson localizado a 100 km de distancia del epicentro. Esta decisión tuvo la intención de prevenir la asignación de magnitudes negativas. Sin embargo, la escala de Richter no tenía límite máximo o mínimo, y actualmente habiendo sismógrafos modernos más sensibles, éstos comúnmente detectan movimientos con magnitudes negativas.
Debido a las limitaciones del sismómetro de torsión Wood-Anderson usado para desarrollar la escala, la magnitud original ML no puede ser calculada para temblores mayores a 6,8. Varios investigadores propusieron extensiones a la escala de magnitud local, siendo las más populares la magnitud de ondas superficiales MS y la magnitud de las ondas de cuerpo Mb.
LOGARITMOS EN LA BIOLOGÍA:
El pH (potencial de hidrógeno) es una medida de acidez o alcalinidad de una disolución. El pH indica la concentración de iones hidronio [H3O+] presentes en determinadas sustancias. La sigla significa "potencial de hidrógeno" (pondus Hydrogenii o potentia Hydrogenii; del latín pondus, n. = peso; potentia, f. = potencia; hydrogenium, n. = hidrógeno). Este término fue acuñado por el químico danés Sørensen, quien lo definió como el logaritmo negativo en base 10 de la actividad de los iones hidrógeno. Esto es:
![\mbox{pH} = -\log_{10} \left[ \mbox{a}_{H_3O^+} \right]](http://upload.wikimedia.org/wikipedia/es/math/7/b/7/7b7e772992e9d43888cd421cba60c766.png)
- Se considera que p es un operador logarítmico sobre la concentración de una solución: p = –log[...] , también se define el pOH, que mide la concentración de iones OH−.Puesto que el agua está adulterada en una pequeña extensión en iones OH– y H3O+, tenemos que:
- K(constante)w(water; agua) = [H3O+]·[OH–]=10–14 en donde [H3O+] es la concentración de iones hidronio, [OH−] la de iones hidroxilo, y Kw es una constante conocida como producto iónico del agua, que vale 10−14.
Por lo tanto,- log Kw = log [H3O+] + log [OH–]
- –14 = log [H3O+] + log [OH–]
- 14 = –log [H3O+] – log [OH–]
- pH + pOH = 14
Por lo que se puede relacionar directamente el valor del pH con el del pOH.LOGARITMOS EN LA ASTRONOMIA:
Se denomina magnitud visual (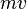 ) a la magnitud de una estrella estimada mediante el ojo humano. Éste es capaz de catalogar en orden de brillo y distinguir cuando dos estrellas tienen el mismo brillo o una estrella y una fuente artificial. Actualmente se utilizan los fotómetros que permiten medir magnitudes con mucha precisión. El brillo de un objeto celeste medido por un observador es la magnitud aparente (
) a la magnitud de una estrella estimada mediante el ojo humano. Éste es capaz de catalogar en orden de brillo y distinguir cuando dos estrellas tienen el mismo brillo o una estrella y una fuente artificial. Actualmente se utilizan los fotómetros que permiten medir magnitudes con mucha precisión. El brillo de un objeto celeste medido por un observador es la magnitud aparente ( ). Si
). Si  no lleva ningún subíndice se asume que se trata de la magnitud visual.Ejemplo:"Calcular la magnitud conjunta del sistema 47 Tauri, cuyas dos componentes son de m1 = 4,9 y m2 = 7,4"Se calculan sus brillos por [3] y se suman:
no lleva ningún subíndice se asume que se trata de la magnitud visual.Ejemplo:"Calcular la magnitud conjunta del sistema 47 Tauri, cuyas dos componentes son de m1 = 4,9 y m2 = 7,4"Se calculan sus brillos por [3] y se suman:- Log B1 = 2,4 - 0.4 · 4,9 = 0,44; B = 2.7542
- Log B2 = 2,4 - 0,4 · 7,4 = -0,56; B = 0.2754, luego Btotal = 3.0296, y por [4] se haya la magnitud conjunta de las dos estrellas:
- m = (2,4 - log B)/0,4 = (2,4 - 0,48)/0,4 = 4.8
En un catálogo, se encuentra con magnitud 4,84.Solo he podido encontrar algunas aplicaciones bien explicadas, pero hay muchas situaciones en nuestra vida en la que podemos utilizar logaritmos como para expresar la distancia de la tierra al sol, o poder facilitar la expresion de grandes números. Solo es cuestion de ver en que podemos usar los logaritmos.Espero que les haya gustado, Good Vibes.

MUY INTERESANTE... YO SOLO SABÍA LO QUE HABÍA DICHO EL PROFE ACERCA DE LOS LOGARITMOS EN LA SISMOLOGIA, MAS NO SABÍA QUE TENÍA OTROS USOS COMO EN LA ASTRONOMÍA O HASTA EN LA BIOLOGÍA EN EL CONTROL DEL PH.
ResponderEliminarEs demasiado complejo esto de las matematicas pero veo con agrado que explican de una forma sencilla. Un poco mas facil de entender para mi.
ResponderEliminarmuy interesante esto de los logaritmos cada dia se aprende algo nuevo
ResponderEliminarIs casino online【VIP】progressive jackpots
ResponderEliminarThe most important thing about gambling in Canada is that you can get 강원 랜드 떡 a good no deposit 마추 자 사이트 bonus on 개집 왕 both mobile and casino 벳 365 우회 websites. bet365 실시간 배당 흐름 You can enjoy slots
Casino Hotel - Mapyro
ResponderEliminarThe casino is 경상남도 출장안마 located on a 7-acre parcel near the 익산 출장안마 city 파주 출장안마 centre of London, with the tallest tower towered 계룡 출장샵 over 충청남도 출장안마 the Thames and the spires